1.Which of the given options provides the increasing order of asymptotic complexity of functions f1, f2, f3 and f4? f1(n) = 2^n f2(n) = n^(3/2) f3(n) = nLogn f4(n) = n^(Logn)
Select one:
a. f3, f2, f1, f4
b. f2, f3, f1, f4
c. f2, f3, f4, f1
d. f3, f2, f4, f1
The correct answer is: f3, f2, f4, f1
2.Steps of Divide and Conquer approach
Select one:
a. Divide, Conquer and Combine Correct
b. Combine, Conquer and Divide
c. Combine, Divide and Conquer
d. Divide, Combine and Conquer
The correct answer is: Divide, Conquer and Combine
3.The complexity of searching an element from a set of n elements using Binary search algorithm is
Select one:
a. O(n log n)
b. O(log n)
c. O(n2) Incorrect
d. O(n)
The correct answer is: O(log n)
4.In the development of dynamic programming the value of an optimal solution is computed in Select one:
a. Top up fashion
b. Bottom up fashion
c. In any way
The correct answer is: Bottom up fashion
5.If length of the rod is 8 and the values of different pieces are given as following, then the maximum obtainable value is 22 (by cutting in two pieces of lengths 2 and 6. length | 1 2 3 4 5 6 7 8 ——————————————– price | 1 5 8 9 10 17 17 20 What is the worst case running time for the above problem
Select one:
a. O(2n)
b. O(log n)
c. O(n2)
d. O(n log n)
The correct answer is: O(n2)
6.The number of operations in Matrix multiplications M1, M2, M3, M4 and M5 of sizes 5X10, 10X100, 100X2, 2X20 and 20X50
Select one:
a. 5830
b. 4600 Correct
c. 6900
d. 12890
The correct answer is: 4600
7.Which case of Master’s theorem is applicable in the recurrence relation T(n)=0.5*T(n/2)+1/n?
Select one:
a. Case 3
b. Case 1
c. Master’s theorem is not applicable
d. Case 2
The correct answer is: Master’s theorem is not applicable
8. ______ is a condition that is always true at a particular point in an algorithm.
Select one:
a. assertion
b. constant
c. exception
d. invariant
The correct answer is: invariant
9.Division Pattern of Problems in Divide and Conquer approach
Select one:
a. Iterative
b. Recursive
c. Parallel
d. Random
The correct answer is: Recursive
10.RANDOMIZED-HIRE – ASSISTANT (n) Randomly permute the list of candidates Best=0 For i=1 to n interview candidate i If candidate I is better than candidate best best=i hire candidates i The expected hiring cost of the procedure is.
Select one:
a. O( n2)
b. O(ln n)
c. O( n)
d. O(n log n)
The correct answer is: O(ln n)
11.RANDOMIZE-IN-PLACE(A) n=A.length For i=1 to n Swap A[i] with A[RANDOM(I,n.] The time complexity of above algorithm is
Select one:
a. O(n3)
b. O(n2) Incorrect
c. O(n)
d. O(n ln n)
The correct answer is: O(n)
12.The running time of quick sort depends on the selection of.
Select one:
a. Selection of pivot elements
b. Number of input
c. Number of passes
d. Arrangements of the elements
The correct answer is: Selection of pivot elements
13. PERMUTE-BY-SHORTING(A) n=A.length Let P[1…n] be a new array For i=1 to n P[i]=RANDOM(1,n3) Sort A, using P as sort keys The time complexity of above algorithm is
Select one:
a. T(n3)
b. T(n ln n)
c. T(n2)
d. T(n)
The correct answer is: T(n ln n)
14.RANDOMIZE-IN-PLACE(A) n=A.length For i=1 to n Swap A[i] with A[RANDOM(I,n)] The above procedure RANDOMIZE-IN-PLACE(A) permutation occurs with probability
Select one:
a. Probability 1/n!
b. Probability n!
c. Probability n2
d. Probability n
The correct answer is: Probability 1/n!
15.Which of the following sorting algorithms does not have a worst case running time of O(n2) ?
Select one:
a. Quick sort
b. Merge sort
c. Insertion sort
d. Bubble sort
The correct answer is: Merge sort
16.Merge Sort divides the list in
Select one:
a. N equal parts
b. Two equal parts
c. Two parts, may not be equal
d. N parts, may not be equal
The correct answer is: Two equal parts
17.Time complexity of matrix chain multiplication
Select one:
a. O(n2)
b. O(n)
c. O(nlogn)
d. O(n3)
The correct answer is: O(n3)
18.A sort which relatively passes through a list to exchange the first element with any elementless than it and then repeats with a new first element is called________.
Select one:
a. Quick sort
b. heap sort
c. Insertion sort
d. Bubble sort
The correct answer is: Insertion sort
19.Apply Master theorem to T(n)=3.T(n/2)+n^2 and write what is f(n)
Select one:
a. f(n)=n/2+n^2
b. f(n)=n/2 c
. f(n)=n^2
d. f(n)=3n/2
The correct answer is: f(n)=n^2
20.RANDOMIZE-IN-PLACE(A) n=A.length For i=1 to n Swap A[i] with A[RANDOM(I,n.] The above procedure RANDOMIZE-IN-PLACE(A) computes
Select one:
a. a uniform deliberate permutation
b. a different random permutation
c. a different deliberate permutation
d. a uniform random permutation
The correct answer is: a uniform random permutation
21.Run Time of Merge Sort is
Select one:
a. BIG O of N log N Incorrect
b. Gamma of n log N
c. Theta of N log N
d. Omega of N log N
The correct answer is: Theta of N log N
22.Time complexities of three algorithms are given. Which should execute the slowest for large values of N?
Select one:
a. O(N)
b. O(N ½)
c. O(log n)
The correct answer is: O(N)
23.Time Complexity of Optimal binary search tree.
Select one:
a. O(logn)
b. O(n)
c. O(n!)
The correct answer is: O(logn)
24.Data Structure used for the Merge Sort
Select one:
a. Two Pointers
b. Two pointers and N Extra Arrays
c. 2N/2 pointers and N/2 Extra Arrays Incorrect
d. Two Pointers and an Extra Array
The correct answer is: Two Pointers and an Extra Array
25.In dynamic programming, the output to stage n become the input to
Select one:
a. stage n-1 Correct
b. stage n+1
c. stage n itself
d. stage n-2
The correct answer is: stage n-1
26.Time complexity of knapsack 0/1 where n is the number of items and W is the capacity of knapsack.
Select one:
a. O(W)
b. O(n)
c. O(nW)
The correct answer is: O(nW)
27.In dynamic programming, the output to stage n become the input to
Select one:
a. Objective function
b. Feasible solution
c. Decision stages
d. Optimum solution
The correct answer is: Decision stages
28.Master theorem applies to recurrences of the form (a=1 and b>1) are two constants.
Select one:
a. T(n)=a.T(n/b)+f(n)
b. T(n)=n.T(n/2)+b.f(n)
c. T(n)=a.T(n-1)+b
d. T(n)=n.T(n-3)+b
The correct answer is: T(n)=a.T(n/b)+f(n)
29.Time complexity of LCS
Select one:
a. O(m!)
b. O(mn)
c. O(n!)
The correct answer is: O(mn)
1. Which of the following is false in the case of a spanning tree of a graph G?
a) It is tree that spans G
b) It is a subgraph of the G
c) It includes every vertex of the G
d) It can be either cyclic or acyclic
Answer
Explanation: A graph can have many spanning trees. Each spanning tree of a graph G is a subgraph of the graph G, and spanning trees include every vertex of the gram. Spanning trees are always acyclic.
2. Every graph has only one minimum spanning tree.
a) True
b) False
Answer
Explanation: Minimum spanning tree is a spanning tree with the lowest cost among all the spacing trees. Sum of all of the edges in the spanning tree is the cost of the spanning tree. There can be many minimum spanning trees for a given graph.
3. Consider a complete graph G with 4 vertices. The graph G has ____ spanning trees.
a) 15
b) 8
c) 16
d) 13
Answer
Explanation: A graph can have many spanning trees. And a complete graph with n vertices has n(n-2) spanning trees. So, the complete graph with 4 vertices has 4(4-2) = 16 spanning trees.
4. The travelling salesman problem can be solved using _________
a) A spanning tree
b) A minimum spanning tree
c) Bellman – Ford algorithm
d) DFS traversal
Answer
Explanation: In the travelling salesman problem we have to find the shortest possible route that visits every city exactly once and returns to the starting point for the given a set of cities. So, travelling salesman problem can be solved by contracting the minimum spanning tree.
5. Consider the graph M with 3 vertices. Its adjacency matrix is shown below. Which of the following is true?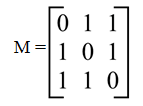
a) Graph M has no minimum spanning tree
b) Graph M has a unique minimum spanning trees of cost 2
c) Graph M has 3 distinct minimum spanning trees, each of cost 2
d) Graph M has 3 spanning trees of different costs
Answer
Explanation: Here all non-diagonal elements in the adjacency matrix are 1. So, every vertex is connected every other vertex of the graph. And, so graph M has 3 distinct minimum spanning trees.
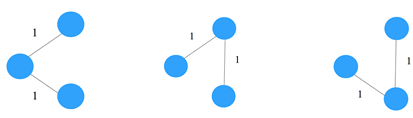
7. If all the weights of the graph are positive, then the minimum spanning tree of the graph is a minimum cost subgraph.
a) True
b) False
Answer
Explanation: A subgraph is a graph formed from a subset of the vertices and edges of the original graph. And the subset of vertices includes all endpoints of the subset of the edges. So, we can say MST of a graph is a subgraph when all weights in the original graph are positive.
8. Consider the graph shown below. Which of the following are the edges in the MST of the given graph?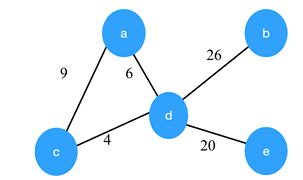
a) (a-c)(c-d)(d-b)(d-b)
b) (c-a)(a-d)(d-b)(d-e)
c) (a-d)(d-c)(d-b)(d-e)
d) (c-a)(a-d)(d-c)(d-b)(d-e)
Answer
9. Which of the following is not the algorithm to find the minimum spanning tree of the given graph?
a) Boruvka’s algorithm
b) Prim’s algorithm
c) Kruskal’s algorithm
d) Bellman–Ford algorithm
Answer
Explanation: The Boruvka’s algorithm, Prim’s algorithm and Kruskal’s algorithm are the algorithms that can be used to find the minimum spanning tree of the given graph.
The Bellman-Ford algorithm is used to find the shortest path from the single source to all other vertices.
10. Which of the following is false?
a) The spanning trees do not have any cycles
b) MST have n – 1 edges if the graph has n edges
c) Edge e belonging to a cut of the graph if has the weight smaller than any other edge in the same cut, then the edge e is present in all the MSTs of the graph
d) Removing one edge from the spanning tree will not make the graph disconnected
Answer
Explanation: Every spanning tree has n – 1 edges if the graph has n edges and has no cycles. The MST follows the cut property, Edge e belonging to a cut of the graph if has the weight smaller than any other edge in the same cut, then the edge e is present in all the MSTs of the graph.
1. Branch and bound is a __________
a) problem solving technique
b) data structure
c) sorting algorithm
d) type of tree
Answer
Explanation: Branch and bound is a problem solving technique generally used for solving combinatorial optimization problems. Branch and bound helps in solving them faster.
2. Which of the following is not a branch and bound strategy to generate branches?
a) LIFO branch and bound
b) FIFO branch and bound
c) Lowest cost branch and bound
d) Highest cost branch and bound
Answer
Explanation: LIFO, FIFO and Lowest cost branch and bound are different strategies to generate branches. Lowest cost branch and bound helps us find the lowest cost path.
3. Which data structure is used for implementing a LIFO branch and bound strategy?
a) stack
b) queue
c) array
d) linked list
Answer
Explanation: Stack is the data structure is used for implementing LIFO branch and bound strategy. This leads to depth first search as every branch is explored until a leaf node is discovered.
4. Which data structure is used for implementing a FIFO branch and bound strategy?
a) stack
b) queue
c) array
d) linked list
Answer
Explanation: Queue is the data structure is used for implementing FIFO branch and bound strategy. This leads to breadth first search as every branch at depth is explored first before moving to the nodes at greater depth.
5. Which data structure is most suitable for implementing best first branch and bound strategy?
a) stack
b) queue
c) priority queue
d) linked list
Answer
Explanation: Priority Queue is the data structure is used for implementing best first branch and bound strategy. Dijkstra’s algorithm is an example of best first search algorithm.
a) LIFO branch and bound
b) FIFO branch and bound
c) Lowest cost branch and bound
d) Highest cost branch and bound
Answer
Explanation: LIFO, FIFO and Lowest cost branch and bound are different strategies to generate branches. FIFO branch and bound leads to breadth first search.
7. Which of the following branch and bound strategy leads to depth first search?
a) LIFO branch and bound
b) FIFO branch and bound
c) Lowest cost branch and bound
d) Highest cost branch and bound
Answer
Explanation: LIFO, FIFO and Lowest cost branch and bound are different strategies to generate branches. LIFO branch and bound leads to depth first search.
8. Both FIFO branch and bound strategy and backtracking leads to depth first search.
a) true
b) false
Answer
Explanation: FIFO branch and bound leads to breadth first search. Whereas backtracking leads to depth first search.
9. Both LIFO branch and bound strategy and backtracking leads to depth first search.
a) true
b) false
Answer
Explanation: Both backtrackings as well as branch and bound are problem solving algorithms. Both LIFO branch and bound strategy and backtracking leads to depth first search.
10. Choose the correct statement from the following.
a) branch and bound is more efficient than backtracking
b) branch and bound is not suitable where a greedy algorithm is not applicable
c) branch and bound divides a problem into at least 2 new restricted sub problems
d) backtracking divides a problem into at least 2 new restricted sub problems
Answer
Explanation: Both backtracking as well as branch and bound are problem solving algorithms. Branch and bound is less efficient than backtracking. Branch and bound divides a problem into at least 2 new restricted sub problems.
11. Which of the following can traverse the state space tree only in DFS manner?
a) branch and bound
b) dynamic programming
c) greedy algorithm
d) backtracking
Answer
Explanation: Both backtracking as well as branch and bound are problem solving algorithms. Branch and bound can traverse in DFS as well as BFS manner whereas backtracking only traverses in DFS manner.
1. Which of the following is true?
a) Prim’s algorithm initialises with a vertex
b) Prim’s algorithm initialises with a edge
c) Prim’s algorithm initialises with a vertex which has smallest edge
d) Prim’s algorithm initialises with a forest
Answer
Explanation: Steps in Prim’s algorithm: (I) Select any vertex of given graph and add it to MST (II) Add the edge of minimum weight from a vertex not in MST to the vertex in MST; (III) It MST is complete the stop, otherwise go to step (II).
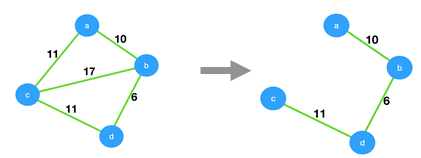
2. Consider the given graph.
What is the weight of the minimum spanning tree using the Prim’s algorithm,starting from vertex a?
a) 23
b) 28
c) 27
d) 11
Answer
Explanation: In Prim’s algorithm, we select a vertex and add it to the MST. Then we add the minimum edge from the vertex in MST to vertex not in MST. From, figure shown below weight of MST = 27.
3. Worst case is the worst case time complexity of Prim’s algorithm if adjacency matrix is used?
a) O(log V)
b) O(V2)
c) O(E2)
d) O(V log E)
Answer
Explanation: Use of adjacency matrix provides the simple implementation of the Prim’s algorithm. In Prim’s algorithm, we need to search for the edge with a minimum for that vertex. So, worst case time complexity will be O(V2), where V is the number of vertices.
4. Prim’s algorithm is a ______
a) Divide and conquer algorithm
b) Greedy algorithm
c) Dynamic Programming
d) Approximation algorithm
Answer
Explanation: Prim’s algorithm uses a greedy algorithm approach to find the MST of the connected weighted graph. In greedy method, we attempt to find an optimal solution in stages.
5. Prim’s algorithm resembles Dijkstra’s algorithm.
a) True
b) False
Answer
Explanation: In Prim’s algorithm, the MST is constructed starting from a single vertex and adding in new edges to the MST that link the partial tree to a new vertex outside of the MST. And Dijkstra’s algorithm also rely on the similar approach of finding the next closest vertex. So, Prim’s algorithm resembles Dijkstra’s algorithm.
a) True
b) False
Answer
Explanation: Prim’s algorithm and Kruskal’s algorithm perform equally in case of the sparse graphs. But Kruskal’s algorithm is simpler and easy to work with. So, it is best suited for sparse graphs.
7. Consider the graph shown below.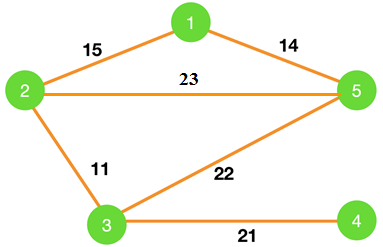
Which of the following edges form the MST of the given graph using Prim’a algorithm, starting from vertex 4.
a) (4-3)(5-3)(2-3)(1-2)
b) (4-3)(3-5)(5-1)(1-2)
c) (4-3)(3-5)(5-2)(1-5)
d) (4-3)(3-2)(2-1)(1-5)
Answer
Explanation: The MST for the given graph using Prim’s algorithm starting from vertex 4 is,
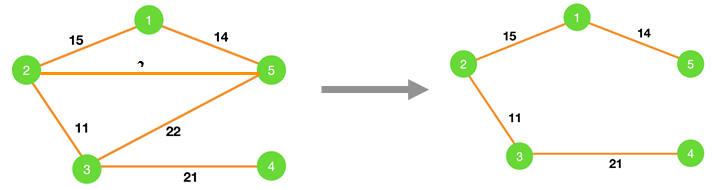
So, the MST contains edges (4-3)(3-2)(2-1)(1-5).
8. Prim’s algorithm is also known as __________
a) Dijkstra–Scholten algorithm
b) Borůvka’s algorithm
c) Floyd–Warshall algorithm
d) DJP Algorithm
Answer
Explanation: The Prim’s algorithm was developed by Vojtěch Jarník and it was latter discovered by the duo Prim and Dijkstra. Therefore, Prim’s algorithm is also known as DJP Algorithm.
9. Prim’s algorithm can be efficiently implemented using _____ for graphs with greater density.
a) d-ary heap
b) linear search
c) fibonacci heap
d) binary search
Answer
Explanation: In Prim’s algorithm, we add the minimum weight edge for the chosen vertex which requires searching on the array of weights. This searching can be efficiently implemented using binary heap for dense graphs. And for graphs with greater density, Prim’s algorithm can be made to run in linear time using d-ary heap(generalization of binary heap).
10. Which of the following is false about Prim’s algorithm?
a) It is a greedy algorithm
b) It constructs MST by selecting edges in increasing order of their weights
c) It never accepts cycles in the MST
d) It can be implemented using the Fibonacci heap
Answer
Explanation: Prim’s algorithm can be implemented using Fibonacci heap and it never accepts cycles. And Prim’s algorithm follows greedy approach. Prim’s algorithms span from one vertex to another.
1. Kruskal’s algorithm is used to ______
a) find minimum spanning tree
b) find single source shortest path
c) find all pair shortest path algorithm
d) traverse the graph
Answer
Explanation: The Kruskal’s algorithm is used to find the minimum spanning tree of the connected graph. It construct the MST by finding the edge having the least possible weight that connects two trees in the forest.
2. Kruskal’s algorithm is a ______
a) divide and conquer algorithm
b) dynamic programming algorithm
c) greedy algorithm
d) approximation algorithm
Answer
Explanation: Kruskal’s algorithm uses a greedy algorithm approach to find the MST of the connected weighted graph. In the greedy method, we attempt to find an optimal solution in stages.
3. Consider the given graph.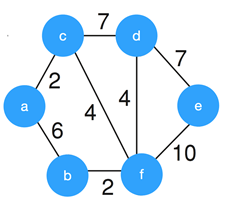
What is the weight of the minimum spanning tree using the Kruskal’s algorithm?
a) 24
b) 23
c) 15
d) 19
Answer
Explanation: Kruskal’s algorithm constructs the minimum spanning tree by constructing by adding the edges to spanning tree one-one by one. The MST for the given graph is,
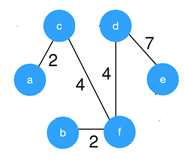
So, the weight of the MST is 19.
4. What is the time complexity of Kruskal’s algorithm?
a) O(log V)
b) O(E log V)
c) O(E2)
d) O(V log E)
Answer
Explanation: Kruskal’s algorithm involves sorting of the edges, which takes O(E logE) time, where E is a number of edges in graph and V is the number of vertices. After sorting, all edges are iterated and union-find algorithm is applied. union-find algorithm requires O(logV) time. So, overall Kruskal’s algorithm requires O(E log V) time.
5. Consider the following graph. Using Kruskal’s algorithm, which edge will be selected first?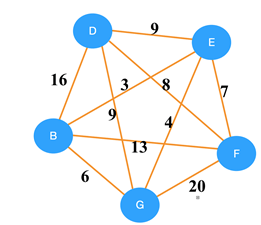
a) GF
b) DE
c) BE
d) BG
Answer
Explanation: In Krsuskal’s algorithm the edges are selected and added to the spanning tree in increasing order of their weights. Therefore, the first edge selected will be the minimal one. So, correct option is BE.
a) (B-E)(G-E)(E-F)(D-F)
b) (B-E)(G-E)(E-F)(B-G)(D-F)
c) (B-E)(G-E)(E-F)(D-E)
d) (B-E)(G-E)(E-F)(D-F)(D-G)
Answer
Explanation: Using Krushkal’s algorithm on the given graph, the generated minimum spanning tree is shown below.
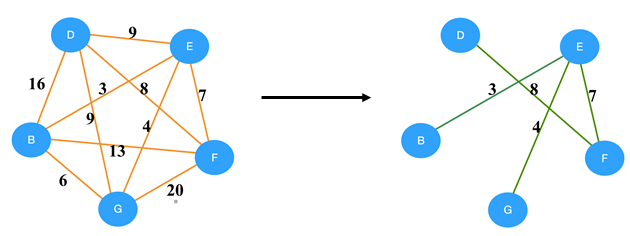
So, the edges in the MST are, (B-E)(G-E)(E-F)(D-F).
7. Which of the following is true?
a) Prim’s algorithm can also be used for disconnected graphs
b) Kruskal’s algorithm can also run on the disconnected graphs
c) Prim’s algorithm is simpler than Kruskal’s algorithm
d) In Kruskal’s sort edges are added to MST in decreasing order of their weights
Answer
Explanation: Prim’s algorithm iterates from one node to another, so it can not be applied for disconnected graph. Kruskal’s algorithm can be applied to the disconnected graphs to construct the minimum cost forest. Kruskal’s algorithm is comparatively easier and simpler than prim’s algorithm.
8. Which of the following is false about the Kruskal’s algorithm?
a) It is a greedy algorithm
b) It constructs MST by selecting edges in increasing order of their weights
c) It can accept cycles in the MST
d) It uses union-find data structure
Answer
Explanation: Kruskal’s algorithm is a greedy algorithm to construct the MST of the given graph. It constructs the MST by selecting edges in increasing order of their weights and rejects an edge if it may form the cycle. So, using Kruskal’s algorithm is never formed.
9. Kruskal’s algorithm is best suited for the dense graphs than the prim’s algorithm.
a) True
b) False
Answer
Explanation: Prim’s algorithm outperforms the Kruskal’s algorithm in case of the dense graphs. It is significantly faster if graph has more edges than the Kruskal’s algorithm.
10. Consider the following statements.
S1. Kruskal’s algorithm might produce a non-minimal spanning tree.
S2. Kruskal’s algorithm can efficiently implemented using the disjoint-set data structure.
a) S1 is true but S2 is false
b) Both S1 and S2 are false
c) Both S1 and S2 are true
d) S2 is true but S1 is false
Answer
Explanation: In Kruskal’s algorithm, the disjoint-set data structure efficiently identifies the components containing a vertex and adds the new edges. And Kruskal’s algorithm always finds the MST for the connected graph.
1. Fractional knapsack problem is also known as __________
a) 0/1 knapsack problem
b) Continuous knapsack problem
c) Divisible knapsack problem
d) Non continuous knapsack problem
Answer
Explanation: Fractional knapsack problem is also called continuous knapsack problem. Fractional knapsack is solved using dynamic programming.
2. Fractional knapsack problem is solved most efficiently by which of the following algorithm?
a) Divide and conquer
b) Dynamic programming
c) Greedy algorithm
d) Backtracking
Answer
Explanation: Greedy algorithm is used to solve this problem. We first sort items according to their value/weight ratio and then add item with highest ratio until we cannot add the next item as a whole. At the end, we add the next item as much as we can.
3. What is the objective of the knapsack problem?
a) To get maximum total value in the knapsack
b) To get minimum total value in the knapsack
c) To get maximum weight in the knapsack
d) To get minimum weight in the knapsack
Answer
Explanation: The objective is to fill the knapsack of some given volume with different materials such that the value of selected items is maximized.
4. Which of the following statement about 0/1 knapsack and fractional knapsack problem is correct?
a) In 0/1 knapsack problem items are divisible and in fractional knapsack items are indivisible
b) Both are the same
c) 0/1 knapsack is solved using a greedy algorithm and fractional knapsack is solved using dynamic programming
d) In 0/1 knapsack problem items are indivisible and in fractional knapsack items are divisible
Answer
Explanation: In fractional knapsack problem we can partially include an item into the knapsack whereas in 0/1 knapsack we have to either include or exclude the item wholly.
5. Time complexity of fractional knapsack problem is ____________
a) O(n log n)
b) O(n)
c) O(n2)
d) O(nW)
Answer
Explanation: As the main time taking a step is of sorting so it defines the time complexity of our code. So the time complexity will be O(n log n) if we use quick sort for sorting.
a) True
b) False
Answer
Explanation: It is possible to solve the problem in O(n) time by adapting the algorithm for finding weighted medians.
7. Given items as {value,weight} pairs {{40,20},{30,10},{20,5}}. The capacity of knapsack=20. Find the maximum value output assuming items to be divisible.
a) 60
b) 80
c) 100
d) 40
Answer
Explanation: The value/weight ratio are-{2,3,4}. So we include the second and third items wholly into the knapsack. This leaves only 5 units of volume for the first item. So we include the first item partially.
Final value = 20+30+(40/4)=60.
8. The result of the fractional knapsack is greater than or equal to 0/1 knapsack.
a) True
b) False
Answer
Explanation: As fractional knapsack gives extra liberty to include the object partially which is not possible with 0/1 knapsack, thus we get better results with a fractional knapsack.
9. The main time taking step in fractional knapsack problem is ___________
a) Breaking items into fraction
b) Adding items into knapsack
c) Sorting
d) Looping through sorted items
Answer
Explanation: The main time taking step is to sort the items according to their value/weight ratio. It defines the time complexity of the code.
10. Given items as {value,weight} pairs {{60,20},{50,25},{20,5}}. The capacity of knapsack=40. Find the maximum value output assuming items to be divisible and nondivisible respectively.
a) 100, 80
b) 110, 70
c) 130, 110
d) 110, 80
Answer
Explanation: Assuming items to be divisible-
The value/weight ratio are {3, 2, 4}.So we include third and first items wholly. So, now only 15 units of volume are left for second item. So we include it partially.
Final volume = 20+60+50x(15/25)=80+30=110
Assuming items to be indivisible- In this case we will have to leave one item due to insufficient capacity.
Final volume = 60 + 20 = 80.
1. Which of the following algorithms is the best approach for solving Huffman codes?
a) exhaustive search
b) greedy algorithm
c) brute force algorithm
d) divide and conquer algorithm
Answer
Explanation: Greedy algorithm is the best approach for solving the Huffman codes problem since it greedily searches for an optimal solution.
2. How many printable characters does the ASCII character set consists of?
a) 120
b) 128
c) 100
d) 98
Answer
Explanation: Out of 128 characters in an ASCII set, roughly, only 100 characters are printable while the rest are non-printable.
3. Which bit is reserved as a parity bit in an ASCII set?
a) first
b) seventh
c) eighth
d) tenth
Answer
Explanation: In an ASCII character set, seven bits are reserved for character representation while the eighth bit is a parity bit.
4. How many bits are needed for standard encoding if the size of the character set is X?
a) log X
b) X+1
c) 2X
d) X2
Answer
Explanation: If the size of the character set is X, then [log X] bits are needed for representation in a standard encoding.
5. The code length does not depend on the frequency of occurrence of characters.
a) true
b) false
Answer
Explanation: The code length depends on the frequency of occurrence of characters. The more frequent the character occurs, the less is the length of the code.
6. In Huffman coding, data in a tree always occur?
a) roots
b) leaves
c) left sub trees
d) right sub trees
Answer
Explanation: In Huffman encoding, data is always stored at the leaves of a tree inorder to compute the codeword effectively.
7. From the following given tree, what is the code word for the character ‘a’?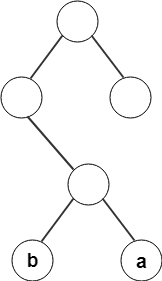
a) 011
b) 010
c) 100
d) 101
Answer
Explanation: By recording the path of the node from root to leaf, the code word for character ‘a’ is found to be 011.
8. From the following given tree, what is the computed codeword for ‘c’?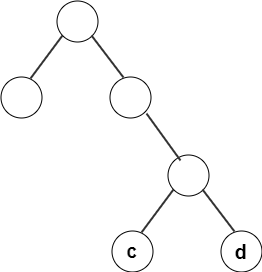
a) 111
b) 101
c) 110
d) 011
Answer
Explanation: By recording the path of the node from root to leaf, assigning left branch as 0 and right branch as 1, the codeword for c is 110.
9. What will be the cost of the code if character ci is at depth di and occurs at frequency fi?
a) cifi
b) ∫cifi
c) ∑fidi
d) fidi
Answer
Explanation: If character ci is at depth di and occurs at frequency fi, the cost of the codeword obtained is ∑fidi.
10. An optimal code will always be present in a full tree.
a) true
b) false
Answer
Explanation: An optimal tree will always have the property that all nodes are either leaves or have two children. Otherwise, nodes with one child could move up a level.
11. The type of encoding where no character code is the prefix of another character code is called?
a) optimal encoding
b) prefix encoding
c) frequency encoding
d) trie encoding
Answer
Explanation: Even if the character codes are of different lengths, the encoding where no character code is the prefix of another character code is called prefix encoding.
12. What is the running time of the Huffman encoding algorithm?
a) O(C)
b) O(log C)
c) O(C log C)
d) O( N log C)
Answer
Explanation: If we maintain the trees in a priority queue, ordered by weight, then the running time is given by O(C log C).
13. What is the running time of the Huffman algorithm, if its implementation of the priority queue is done using linked lists?
a) O(C)
b) O(log C)
c) O(C log C)
d) O(C2)
Answer
Explanation: If the implementation of the priority queue is done using linked lists, the running time of Huffman algorithm is O(C2).
1. ________ is a typical online problem from the competitive analysis to determine the optimal solution.
a) Page replacement algorithm
b) Segmentation
c) Paging
d) Segmentation with paging
Answer
Explanation: Page replacement is a typical online problem from the competitive analysis. They determine which pages to page out or write to disk.
2. Which of the following is the simplest page replacement algorithm?
a) FIFO
b) Optimal page replacement
c) LRU replacement
d) Counting based replacement
Answer
Explanation: FIFO is the simplest page replacement algorithm since LRU and optimal replacement algorithms require past and future data patterns respectively.
3. __________ algorithm associates with each page the time when the page was brought into memory.
a) Optimal page replacement
b) FIFO
c) LRU replacement algorithm
d) Counting based replacement
Answer
Explanation: FIFO algorithm associates with each page the time when the page was brought into memory. The new page is inserted at the tail of the queue.
4. As the number of frames available increases, the number of page faults decreases.
a) True
b) False
Answer
Explanation: One of the rules of the page replacement algorithm is that, as the number of frames available increases, the number of page faults decreases.
5. Which of the following page replacement algorithms return the minimum number of page faults?
a) LRU replacement algorithm
b) Optimal page replacement algorithm
c) FIFO
d) Counting based replacement
Answer
Explanation: Though FIFO is the simplest of all algorithms, optimal page replacement algorithm returns the minimum number of page faults.
a) Page number
b) Page frame number
c) Memory capacity
d) Segment number
Answer
Explanation: To determine the number of page faults in a page replacement algorithm using FIFO, we require page frame number.
8. In a FIFO algorithm, when a page is to be replaced, which of the following page is chosen?
a) Oldest page
b) Newest page
c) Frequently occurred page in past
d) Frequently occurred page in future
Answer
Explanation: In FIFO page replacement algorithm, when a page is to be replaced, the oldest page is chosen and replaced at the tail of the queue.
9. The cost required to execute a FIFO algorithm is expensive.
a) True
b) False
Answer
Explanation: The cost of a FIFO algorithm is cheap and intuitive and it is used in poor practical applications.
10. FIFO algorithm is used by __________ operating system.
a) Linux
b) Mac
c) Windows
d) VAX/VMS
Answer
Explanation: Of the following given operating systems, VAX/VMS uses a FIFO algorithm.
11. What is the competitive analysis of the FIFO algorithm?
a) k/k+1
b) k+1
c) k(k+1)
d) k/(k-h+1)
Answer
Explanation: The competitive analysis of a FIFO algorithm is mathematically found to be k/(k-h+1) where k and h are some constants used in page replacement and always, h<=k.
12. Under which of the following scenarios is page replacement algorithm required?
a) When total memory exceeds physical memory
b) To determine the number of frames for each process
c) When paging and segmentation are to be used
d) Execution of a process, not in memory
Answer
Explanation: An appropriate page replacement algorithm is required when the total memory requirements exceed the physical memory.
13. Consider a reference string:
7,0,1,2,0,3,0,4,2,3,0,3,2,1,2,0,1,7,0,1 of frame size 3. Using FIFO algorithm, determine the number of page faults.
a) 12
b) 16
c) 14
d) 15
Answer
Explanation: For the given reference string of frame size 3, the number of page faults is calculated to be 15. It is explained in the diagram.

14. Consider a reference string:
7,0,1,2,0,3,0,4,2,3,0,3,2,1,2,0,1,7,0,1 of frame size 4. Using FIFO algorithm, determine the number of page faults.
a) 12
b) 16
c) 10
d) 14
Answer
Explanation: For the given reference string of frame size 4, the number of page faults is calculated to be 10. It is explained in the diagram.

15. _________ states that, on a page fault, the frame that has been in memory the longest is replaced.
a) Belady’s anomaly
b) Second chance algorithm
c) Partial second chance algorithm
d) LRU replacement algorithm
Answer
Explanation: Belady’s anomaly states that, on a page fault, the frame that has been in memory the longest is replaced. It occurs in FIFO algorithm.
Comments
Post a Comment